citazione:
"La ricerca scientifica consiste nel vedere quello che tutti gli altri hanno visto, pensando quello che nessun altro ha pensato" Albert Szent Gyorgy (1893-1986) biochimico ungherese.
Premessa:
E' ormai chiaro a tutti gli scienziati che i sensi dell'uomo percepiscono una realtà limitata di ciò che lo circonda, limitata dal range di sensibilità dei propri organi sensoriali: l'occhio percepisce solo alcune lunghezze delle onde elettromagnetiche (quelle del campo visibile), stesso dicasi per l'orecchio.
Restano esclusi dall'indagine diretta i fenomeni fisici che avvengono nelle dimensioni del molto piccolo rispetto alle nostre dimensioni corporali o del molto lontano, così come del molto veloce, e nel contempo, del molto lento.
Quasi tutti i successi della scienza recente si sono realizzati perché l'uomo si è dotato di strumenti che hanno esteso i sui sensi a partire dal telescopio del mitico Galilei. Eppure molti uomini, ancor oggi restano ancorati alle proprie percezioni sensoriali come l'unica fonte di conoscenza della realtà, con questo rinunciando alla modernità del pensiero scientifico che come un investigatore poliziesco indaga con strumenti tecnologici su una realtà di cui sono sfuggite le prove, con strumenti che espandono nel tempo e nello spazio le sue capacità sensoriali.
Ecco il senso, di rallentare la visione del fenomeno balistico dell'asta lanciata da un arbaléte che non riusciremmo a cogliere col nostro occhio, di fermare il tempo nel "fermo immagine" di una videocamera che ci consenta di ragionare, di riflettere, sulle semplici leggi della Fisica classica newtoniana, per ricostruire come un puzzle il "perché accade ciò che accade".
Il mio studio sulla balistica delle aste degli arbalétes iniziato nel 2004 si fonda sul metodo scientifico che si contrappone al metodo pratico-speculativo di altri appassionati pescatori subacquei che si sono cimentati su questo argomento.
Il metodo scientifico introdotto da Galilei parte dalla centralità dell'osservazione del fenomeno fisico che si vuole studiare avendo cura di minimizzare la componente soggettiva della percezione del ricercatore (osservazione riproducibile anche da altri).
Questo metodo, cui fa riferimento ormai tutta la scienza contemporanea, procede ad una misurazione di tutte le variabili fisiche che caratterizzano il fenomeno, quindi dà seguito ad una verifica dei dati sperimentali.
L'indagine ha una sua fase sublime, ovvero, la comprensione dell'essenza dell'esperimento, che nel caso dell'asta lanciata nell'acqua, è quella di un fenomeno fisico dissipativo.
Mi scuso con i lettori più colti per questa premessa che può risultare pedante ma è necessaria dato che su riviste cartacee e su Internet si continuano a pubblicare conclusioni che hanno il sapore dell'invenzione del moto perpetuo, con aste di arbalétes che raggiungono velocità inaudite.
Ho ritenuto necessario perciò scrivere ancora un saggio per ricondurre le convinzioni sulla balistica degli arbalétes in un alveo scientifico.
In questo scritto divulgativo condurrò una prima analisi sotto il profilo della meccanica classica, quindi secondo un punto di vista termodinamico.
1) Il tiro di un arbaléte:
La scienza che s'incarica di studiare il fenomeno balistico in questione è la fluidodinamica, una branca della Fisica che studia il comportamento dei fluidi
(liquidi e gas) in movimento. E' una scienza complessa le cui leggi fondamentali sono riassunte nelle :
Equazione di continuità detta anche della conservazione della massa.
Legge di conservazione della quantità di moto.
Legge di conservazione dell'energia.
Nel caso dell'asta che attraversa l'acqua ci troviamo di fronte ad un fluido viscoso incompressibile, il cui moto relativo rispetto all'asta è particolarmente dissipativo per la viscosità del mezzo.
Uno studio rigoroso e completo richiederebbe l'applicazione al moto dell'asta delle equazioni di Navier-Stokes (equazioni differenziali alle derivate parziali non lineari) ricavate dalle leggi fondamentali citate, equazioni non risolvibili tranne che in alcuni casi limitati con metodi computazionali.
Non è mia intenzione perciò ricavare le equazioni di moto dell'asta neppure in forma semplificata, bensì comprendere il fenomeno fisico per una valutazione qualitativa-sperimentale delle resistenze idrodinamiche in atto e attraverso il fermo immagine dei filmati ad alta velocità capire dove l'ingegnere può intervenire per ridurne gli effetti.
A questo scopo, in questo paragrafo, mi limiterò ad indagare sulla balistica dell'asta applicando la sola legge di conservazione dell'energia al sistema fucile + pescatore + acqua circostante tra l'istante prima di tirare il grilletto e l'istante nel quale l'archetto abbandona l'asta, quindi discutendo il bilancio energetico della balistica interna.
In questo breve intervallo di tempo, l'energia potenziale elastica si trasforma in lavoro che l'archetto (collegamento degli elastici all'asta) compie sull'asta .
Il lavoro eseguito è un semplice "trasferimento" dell'energia, da potenziale elastica a cinetica dell'asta, tuttavia questo non è il solo fenomeno che riguarda il nostro sistema di riferimento, infatti , il fucile rincula e gli elastici archetto compreso, spingendo l'asta spostano le molecole dell'acqua che li circondano. Il bilancio energetico in un sistema di riferimento (di osservazione del fenomeno) esterno al pescatore col fucile immerso nell'acqua, è:
Energia pot. el. = Energia cinetica (asta+archetto+elastici)+
+Energia cinetica delle masse rinculanti+
+Energia cinetica delle molecole d'acqua
Discuto questo bilancio energetico, da un punto di vista generale senza approfondire in questa fase l'essenza del fenomeno fluidodinamico,:
L'energia potenziale elastica: è quella effettivamente disponibile, che non è certo descritta dalla relazione Energia pot.el.= cost. x allungamento el.² (ottenuta dalla legge di Hooke: Forza elastica= cost.x allungamento ) come si legge in alcune pubblicazioni sull'argomento. Per gli elastomeri il diagramma sperimentale sforzo allungamento mostra una dipendenza non lineare della forza dall'allungamento (come è invece nella legge di Hooke), sia nella fase di carico e ancor più nella fase di scarico dell'elastomero, con una grande variabilità delle curve di riferimento tra vari tipi di elastomeri presi in esame.
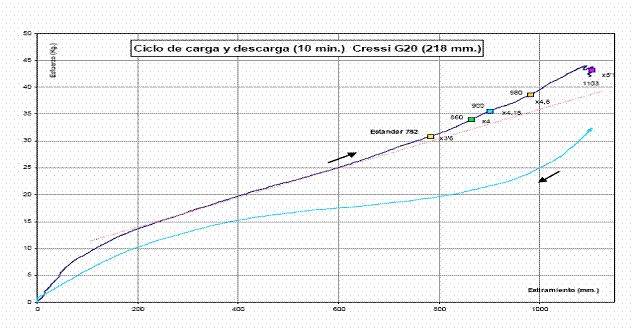
Il diagramma sperimentale riportato sopra, mostra l'andamento reale del ciclo carico- scarico (dopo 10 min) di uno spezzone di elastomero da 218 mm
L'energia disponibile al lancio dell'asta per un certo allungamento dello spezzone elastico è quella sottesa dalla curva di scarico azzurra, che varia (abbassandosi ulteriormente sulle ascisse perdendo energia) se ad esempio il fucile resta carico per un tempo maggiore di 10 min.
In conclusione l'energia potenziale elastica immagazzinata da un arbaléte è indefinibile anche sperimentalmente se non attraverso tabelle approssimative in funzione del tipo di elastomero, della sua lunghezza e del tempo che resta allungato (la variazione non è modesta o trascurabile).
Energia cinetica (asta+archetto+elastici): è l'incognita che vogliamo ricavare dal bilancio energetico dalla quale separando l'energia cinetica dell'archetto e degli elastici si può ricavare l'energia cinetica dell'asta.
Energia cinetica delle masse rinculanti: è un'energia non trascurabile che viene sottratta all'energia potenziale elastica per il lancio dell'asta. Che non sia trascurabile è nell'esperienza di ciascuno di noi: basta effettuare il tiro con il fucile appoggiato su uno scoglio per ottenere un lancio incredibile che può anche rompere la sagola di collegamento all'asta, in questo caso avremmo azzerato l'energia di rinculo che, approssimativamente, nei casi reali è sempre superiore al 10% di quella disponibile.
Poiché si tratta di un'energia cinetica, qual è la massa da attribuire al rinculo del fucile nel caso di un pescatore che tira da una qualunque posizione, e quale sarà la velocità di arretramento non essendo una variabile indipendente dipendendo oltre che dalla massa del fucile anche da una quota della massa del tiratore, variabile ad ogni tiro?
La massa e velocità di rinculo sono indefinibili, e dobbiamo concludere che anche questa quota del bilancio energetico resta indefinita!
Energia cinetica delle molecole d'acqua spostate dalle masse in movimento: è l'energia dissipata dal fenomeno balistico che nel tiro ad esaurimento in una vasca sufficientemente lunga è la totalità dell'energia potenziale elastica disponibile, mentre per gittate minori (tali da garantire una residua energia di impatto sul pesce) è una parte consistente dell'energia pot. el., sfido chiunque a quantificarla con qualunque metodo di calcolo non sperimentale dipendendo (e lo vedremo in seguito) in funzione dello spazio percorso dall'asta, ma anche da un insieme di fattori geometrici di forma dell'asta.
Questa energia è visibile, chiaramente, ad occhio nudo osservando le bollicine di gas prodotte dalla cavitazione che restano in sospensione nell'acqua dopo il tiro nella vasca di prova, visibile ancor più chiaramente nei fermo immagine delle riprese ad alta velocità come effetto scia e cavitazione intorno all'asta e agli elastici.
In conclusione, il bilancio energetico che ho impostato all'inizio, anche per i volenterosi, resta puramente qualitativo e non può essere quantificato in alcun modello fisico-matematico a meno di semplificazioni che inficiano la veridicità dei risultati.
La proposizione che la velocità " Vmax " dell'asta alla fine del lancio sia
Vmax =√ 2 Ep / Masta
Come si legge in alcune pubblicazioni è un'ipotesi talmente semplificata da snaturare il fenomeno, infatti descrive il lancio di un'asta :
nel vuoto assoluto (non in un fluido viscoso) in assenza di rinculo con un elastomero ideale privo di isteresi.
Esclusa la strada del modello fisico-matematico, il mio metodo di studio sperimentale ha preferito misurare direttamente la velocità media dell'asta anche in tratti di traiettoria molto brevi con l'uso di hi-speed camera dalla quale ricavare l'energia cinetica reale dell'asta.
Introdotta questa grandezza nel bilancio energetico ho potuto indagare su valori più attendibili sia dell'energia dissipata dalle resistenze idrodinamiche, sia sull'energia di rinculo per cercare di ottimizzare l'impiego dell'energia disponibile.
2) L'entropia del sistema "arbaléte che lancia l'asta" immerso nell'acqua:
L'asta di un arbaléte ha delle forti similitudini con l'esperimento condotto da Joule verso la fine del 1800 per determinare l'equivalente meccanico del calore, lo riassumo:
In un serbatoio termicamente isolato pieno d'acqua, un sistema di pale mosse da un albero, trasformava l'energia potenziale di un peso posto ad una determinata altezza, in agitazione delle molecole dell'acqua. Joule misurò il conseguente innalzamento della temperatura dell'acqua stabilendo l'equivalenza tra l'energia potenziale del peso e il calore scambiato con l'acqua.
In una vasca isolata termicamente e sufficientemente lunga da contenere la gittata massima dell'asta libera di un arbaléte (una decina di metri) se, con un termometro molto sensibile misurassimo di quanto si è alzata la temperatura dell'acqua dopo un tiro, scopriremmo che tutta l'energia potenziale degli elastici che abbiamo allungato si è trasformata nel riscaldamento dell'acqua della vasca che, in ricordo dell'esperimento citato, nel linguaggio fisico viene chiamato: "effetto Joule".
Il lettore a questo punto si chiederà perché introdurre un'analisi entropica del fucile ad elastici immerso nell'acqua e che cos'è l'entropia.
L'entropia, spiegata volgarmente, è una misura della "qualità dell'energia" : più bassa è l'entropia "E", più alta è la forma di energia.
Fisicamente si definisce ΔE = ΔQ / T
La variazione dell'entropia ΔE di un sistema è il rapporto tra l'energia trasferita mediante calore ΔQ e la temperatura assoluta alla quale avviene il trasferimento T.
L'asta lanciata da un arbaléte è un fenomeno fisico molto particolare che va indagato anche secondo l'aspetto entropico infatti ripercorrendo il ciclo di un tiro scopriremmo che i legami chimici disordinati dell'elastomero nel suo allungamento si "stirano" allineandosi ordinatamente nel senso longitudinale. Questa è la nostra condizione di partenza per il tiro.
Quando l'elastomero inizia a contrarsi i legami delle molecole ritornano in una fase disordinata, questa trasformazione energetica è in parte una trasformazione da energia potenziale elastica in energia cinetica della massa dell'elastomero, che non farebbe aumentare o diminuire l'entropia, se non scoprissimo che alla trasformazione si aggiunge uno scambio termico con l'esterno alla massa elastica, in sostanza, l'accorciamento dell'elastico produce uno scambio di calore con l'acqua circostante perché è aumentata l'energia interna dell'elastico.
Questo fenomeno sfugge alla percezione del subacqueo, ma se egli si mettesse ad allungare ed accorciare l'elastico in aria diverse volte (l'aria non è un buon conduttore del calore) si accorgerebbe che l'elastico "si è scaldato" ovvero ha raggiunto una temperatura più alta dell'ambiente circostante e cede calore alla sua mano.
In conclusione nella sua contrazione l'elastico ha dissipato parte della sua energia potenziale elastica in un ΔQ (uno scambio di calore con l'esterno) aumentando l'entropia del sistema "fucile+asta+acqua circostante".
Chi volesse visualizzare questa energia persa (per il nostro scopo balistico) è l'area racchiusa del ciclo di isteresi del diagramma sperimentale sforzo -allungamento, tra la curva blu di carico e la curva azzurrina dello scarico dello spezzone elastico.
Il degrado della qualità dell'energia è l'idea sublime contenuta nella seconda legge della termodinamica.
L'elastico passa dal disordine delle sue catene polimeriche, all'ordine dell'allungamento di questi legami(l'entropia diminuisce), nel successivo accorciamento si torna al disordine scambiando calore con l'esterno (l'entropia aumenta)
Già nel fenomeno fondamentale dell'arbaléte ovvero nell'accorciamento dell'elastico che spinge l'asta non si conserva l'energia meccanica. Nel bilancio termodinamico dell'elastomero dovremmo scrivere Epotenziale = E cinetica asta+ ΔQ1.
L'elastico che si accorcia nell'acqua oltre a scambiare con l'elemento liquido la sua Energia Interna attraverso il ΔQ1 del bilancio termodinamico riportato sopra si muove in un liquido viscoso soggetto ad attrito superficiale e ad una resistenza idrodinamica di forma che comporta agitazione delle molecole d'acqua in corrispondenza delle sporgenze e della coda dello spezzone elastico.
Quindi dovremo riscrivere il bilancio termodinamico:
Epotenziale = E cinetica asta+ ΔQ1+ ΔQ2
Con ΔQ2 il calore scambiato per effetto delle resistenze idrodinamiche sull'elastomero.
A questo punto, per non essere pedante, lascio al lettore proseguire il bilancio termodinamico per tutte le altre conseguenze dell'accorciamento dell'elastico (rinculo e resistenze idrodinamiche sull'asta e sulle parti rinculanti).
Ho introdotto nello studio del fenomeno balistico il secondo principio della termodinamica con una sua enunciazione particolare per dimostrare anche attraverso un altro metodo di indagine (termodinamico) la validità delle conclusioni del paragrafo precedente
Da uno stato energetico "ordinato": fucile carico di energia potenziale elastica, giungiamo al disordine delle molecole d'acqua.
Ecco riassunto il fenomeno balistico in esame.

